Recursion is a very powerful concept that remains strangely underutilized, even by experienced developers. To the extent that one reads about it, the most common example is an extremely trivial one that is also somewhat misleading. In this chapter, we will look at how recursion can be used to implement tasks that many developers need to carry out on a regular basis.
The definition of code recursion is when a subroutine or function calls itself, either directly or indirectly. However, that is only one piece of the puzzle, so to say. Recursive programming is most useful when coupled with a concept that is even less well understood that recursive code. And, that is the recursive data structure or the recursive mathematical function. Basically, a business (or scientific) problem is best solved with a recursive algorithm when the associated data structure is itself recursive in nature.
In this section we look at the definition of both recursive code and recursive data.
Recursion is defined as the case where a subroutine (or function) calls itself, either directly or indirectly, as in Table 1. In the direct recursion example, the subroutine, named DirectRecursion, carries out some initial processing and calls itself if the current value of its argument, x, is less than zero. Implicit in this is the requirement that at some point the value of x will indeed be greater than or equal to zero. When that happens, the function will no longer call itself and will exit.
In the indirect recursion example, the subroutine IndirectRecursion1 conditionally calls IndirectRecursion2, which conditionally calls IndirectRecursion1 back. Once again, there is an implicit requirement that at some point the subroutine will stop calling itself and all the nested calls will exit.
|
Sub DirectRecursion(x) '... If x < 0 Then DirectRecursion (-x) Else '... End If End Sub |
Sub IndirectRecursion1(x) '... If x < 0 Then IndirectRecursion2 (-x) Else '... End If
End Sub Sub IndirectRecursion2(x) '... If x = Int(x) Then '... Else IndirectRecursion1 (Int(x)) End If End Sub |
Table 1
What does it mean for a subroutine to call itself? The call stack for the DirectRecursion subroutine is in Figure 1. Note that the start point is the testDirectRecursion subroutine. It called DirectRecursion with a negative argument. As a result, DirectRecursion called itself after changing the value of the argument to positive. This, the 2nd call to DirectRecursion, would have a positive value of the argument x and, consequently, would not call itself again. Instead, it would execute the Else clause of the If statement as shown in Figure 2
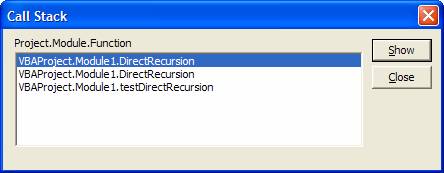
Figure 1


Figure 2
As overlooked as recursive procedures are, even more overlooked are recursive data structures. And, that is particularly confusing since we deal with such structures on a daily basis. A family tree is a recursive data structure, as is an organizational chart. When using a computer, a recursive structure that every one of us interacts with on a regular basis is how files are organized in nested directories on a disk. All these structures are a particular form of a generic data structure known as a tree. In Computer Science, a tree has a large number of applications. We will see one in this chapter; elsewhere in this book, a binary tree serves as the foundation of a rather efficient sort procedure.
Continuing the example of recursive data structures…within the realm of MS Office applications, the implementation of sub-menus is – yes, you guessed it – recursive in nature! As we will see later in this chapter, a sub-menu is a commandbar embedded in a popup control that is part of a parent commandbar.
Finally, there are mathematical functions that are easily defined in a recursive fashion. For example, the recursive definition of the factorial function is n! = n*(n-1)!, where n is a positive integer, and 1!=1. In fact, one could argue that it is only in the context of a recursive data structure that it makes sense to consider a recursive procedure.
In this section, which constitutes the bulk of the chapter, we look at how to understand, develop, and code recursion. The easiest to start with is the trivial example that is probably the most frequently cited example of recursion – the factorial function. After a quick look at it, we will address more practical functions.
This function, as noted above, is recursively defined as n! = n*(n-1)!, where n is a positive integer, and 1!=1. Effectively, n!=1*2*3*…*(n-1)*n. The latter definition should help the reader think of an alternative to the recursive function shown in Code Sample 1.
Function Factorial(ByVal n As Integer)
'returns the factorial of a positive integer; should handle _
values of n upto 170, after which the result is too large _
for even a double to hold.
If n > 1 Then
Factorial = n * Factorial(n - 1)
ElseIf n = 1 Then
Factorial = 1
Else
Factorial = CVErr(xlErrNum)
End If
End Function
For values of n larger than 1, the function calculates the returned value as n multiplied by the factorial of n-1. The recursion stops when n becomes 1, at which time the function simply returns the value 1. This, the factorial function, is probably the most common example of a recursive function. While it is true that the factorial function can be easily implemented without incurring the overhead associated with recursion, it remains an elegantly simple way to introduce and understand the concept of recursion. One very important structural aspect of a recursive routine is illustrated by the If statement in the function. Every properly written recursive function will have one particular conditional clause somewhere in the code. This clause will decide whether to call the routine again (with appropriately adjusted arguments) or to simply return without any further recursive calls. In the Factorial example, this conditional test is the value of n. If it equals 1, no further recursion is needed. If, on the other hand, n>1 then the function calculates the returned value as n * value returned by the recursive call with an argument of n-1. In this particular example, we have one more part of the If statement. It protects against a negative starting value of n. This last error trap may or may not appear in every recursive code.
Next, we shift our attention to a recursive data structure, the most common of which is probably the tree. While the generic tree might come across as little more than an exercise in theory with not much practical value, nothing could be further from the truth. We use a tree every time we access a file on our computer. The structure of files and directories on a computer disk, for all practical purposes, is a tree; as is a family tree and the hierarchical nature of most organizations. The general tree looks as in Figure 3
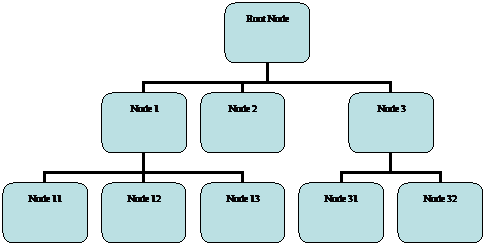
Figure 3
Each node contains some data (not shown in the figure) and a link to its ‘child nodes.’ Such a structure is easily implemented as a class module named Tree – as shown in Code Sample 2. Note the data type of the array Children. It is of type Tree, which is the name of the class module that contains the definition in the first place! This declaration lays the foundation for a recursive data structure.
Option Explicit
'This code goes in a class module named Tree. It sets up a recursive _
data structure since each tree node can have an arbitrary number of _
child nodes, each of which is itself a tree node.
Dim vNodeData As Variant
Dim Children() As Tree
That’s it. That’s all that is needed to declare a tree data structure. Of course, there’s more code to access and update the various elements, but in terms of declarations, the above code is all that is needed!
From this generic tree it is possible to derive a large number of more practical and useful trees. A node of the structure describing files and directories on a disk would store an array of file names in the variant vNodeData, and each element of Children would be a subdirectory node. In an organizational chart, the variant data item would contain information about the person (name, title, department, etc – effectively, a user-defined type or another class itself), and the Children array would refer to the people who report to this individual.
There are many specialized derivatives of this generic tree. One such derivative is a tree in which each node has no more than 2 children. Called a binary tree, the Children array is replaced by two properties, LeftNode and RightNode. Of the many uses of a binary tree, one is to sort a data structure. An example is <<here??>>
One of the more difficult aspects of using recursive
structures and recursive code is building the connections between recursive and
non-recursive components. While
recursive code might be short and simple, at some point it must interact with a
human-compatible interface, which typically is not recursive. The code in the next example below
illustrates some of the issues that one must watch for in developing such an
interface.
In this example, the idea is to build a recursive routine that lists all the files in a folder as well as all the files in all the subfolders of that folder nested as deep as necessary. As Figure 4 illustrates, the result will start in cell A2 of the active worksheet. For each folder we want the full name (i.e., path and name); for each file we want just the name. In addition, for each sub-folder we encounter, the resulting names should be indented one more column to the right.
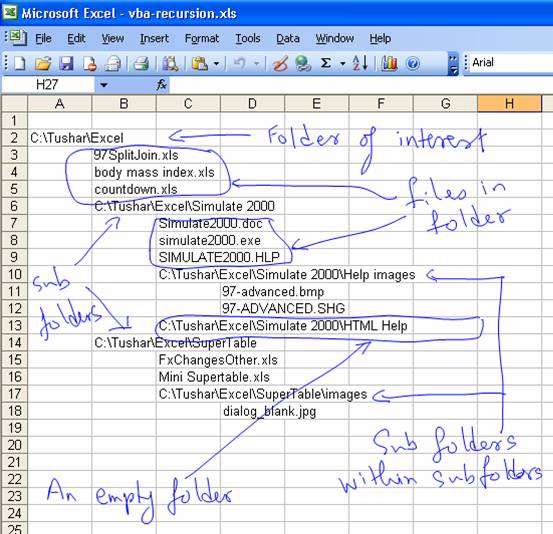
Figure 4
The recursive code for the program is in Code Sample 3. Unlike the factorial example, the non-recursive version of this code would be much more difficult to write, understand, or maintain. The core code is very simple and is contained in the DoOneFolder subroutine. For the folder that is its argument, it writes the name of that folder. Then, it writes the names of each of the files in the folder. Finally, for each subfolder, it calls itself using the subfolder as the argument. That’s it. This simple routine will list all the files in all the subfolders of the specified folder, irrespective of the depth of the file structure!
Of course, the somewhat more complicated task of taking the recursive code and making it interact with a non-recursive worksheet has been left out. Also missing from the code are any protective measures. So, it is possible that folders nested to a depth of 255 or more will cause the program to try and use column 257. Or, if the total number of files and folders in the starting directory exceeds 65,535, the program will try and use a row that does not exist. The example on the CD contains a version that includes the code to trap such errors.
Sub DoOneFolder(aFolder As Folder)
Dim OneSubFolder As Folder, _
aFile As File
'writeOneName aFolder
For Each aFile In aFolder.Files
'writeOneName aFile
Next aFile
For Each OneSubFolder In aFolder.SubFolders
DoOneFolder OneSubFolder
Next OneSubFolder
End Sub
Sub ListAllFiles()
Dim FSO As Scripting.FileSystemObject
Set FSO = New Scripting.FileSystemObject
DoOneFolder FSO.GetFolder("c:\tushar\excel")
End Sub
OK, so how about actually writing the names to the worksheet? What changes do we have to make to make that happen? Before tackling the code, it would help to understand the underlying logic. Every time we write a name, either of a file or a folder, we need to remember to use the next row for the next name. So, we start with a variable with an initial value of 2 (corresponding to the row for cell A2) and we increment it by 1 each time the writeOneName routine writes any name. Next, we look at how to manage the nesting of subfolders. We know that the name of a given folder will be in some column (doesn’t really matter which column). Then, the names of all the files and the immediate subfolders will be in the column one to the right. When we process each of these subfolders, the same logic will apply. Basically, we must increment the column number by 1 each time we step down a node of the sub-tree. And, we should save the current column number so that when we are done processing a sub-tree, the column number is correct for the current folder. This behavior is analogous to that of an argument passed by value to a subroutine.[1]
We start by modifying the procedure that starts it all off – ListAllFiles. Since we must remember the row number irrespective of what subfolder or subtree we are process, it would be appropriate to use a variable– call it RowNbr. However, since the column number is incremented only when the nesting level increases, we don’t need a variable for it. The reason will become apparent when we see the definition of DoOneFolder.
Sub ListAllFiles()
Dim FSO As Scripting.FileSystemObject, RowNbr As Integer
Set FSO = New Scripting.FileSystemObject
RowNbr = 2
DoOneFolder FSO.GetFolder("c:\tushar\excel"), RowNbr, 1
End Sub
Next, we look at the changes in DoOneFolder. It has two new arguments: a ByRef RowNbr and a ByVal ColNbr. The ByRef argument means that the code will update the same variable that was passed to it, i.e., the variable declared in ListAllFiles. However, the reader will remember from Chapter xxx that the ‘by value' declaration of ColNbr means that for all practical purposes the compiler creates a temporary variable available within the scope of DoOneFolder. This means that when the program exits the DoOneFolder procedure, the temporary copy of ColNbr will be discarded and the previous value restored! In other words, each time the nesting level increases ColNbr increases, and each time the nesting level decreases, so does ColNbr.
Sub DoOneFolder(aFolder As Folder, ByRef RowNbr As Integer, _
ByVal ColNbr As Integer)
Dim OneSubFolder As Folder, _
aFile As File
writeOneName aFolder, RowNbr, ColNbr
For Each aFile In aFolder.Files
writeOneName aFile, RowNbr, ColNbr + 1
Next aFile
For Each OneSubFolder In aFolder.SubFolders
DoOneFolder OneSubFolder, RowNbr, ColNbr + 1
Next OneSubFolder
End Sub
In the code above, the first call to writeOneName is to write the name of the current folder. That goes into the actual column specified by the ColNbr argument. Then, while writing out the names of all the files in the folder, the column number is incremented by 1. Finally, while processing each of the subfolders, the incremented value of the ColNbr is passed to the procedure.
Of course, the final piece of the puzzle is the writeOneName subroutine:
Function writeOneName(ByVal FileOrFolder As Object, _
ByRef RowNbr As Integer, ByVal ColNbr As Integer)
If TypeOf FileOrFolder Is Folder Then
ActiveSheet.Cells(RowNbr, ColNbr).Value = _
FileOrFolder.Path
RowNbr = RowNbr + 1
Else
ActiveSheet.Cells(RowNbr, ColNbr).Value = _
FileOrFolder.Name
RowNbr = RowNbr + 1
End If
End Function
Since every subroutine (ListAllFiles and DoOneFolder) passes RowNbr by reference, incrementing its value in the writeOneName subroutine is the equivalent of updating the variable declared in ListAllFiles.
Implementing a submenu item such as the commands under Filter ► is no more difficult than implementing a menu item such as Form… This is because a sub-menu is nothing more than a command bar in the first place.
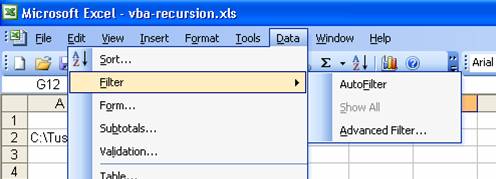
Figure 5
Note that the main menu bar (containing the menus File, Edit, View, etc.) is actually just a docked command bar. To reveal its true nature move the mouse to the left edge of the menu bar, click and drag to undock the bar (see Figure 6).
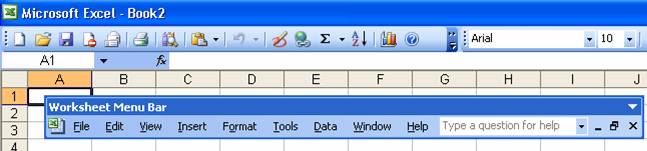
Figure 6
In all Office applications except Excel, the main menu bar is named Menu Bar. In Excel when a chart is the active object, the main menu bar is the Chart Menu Bar. In those instances when a worksheet component is the active object, the main menu bar is the Worksheet Menu Bar. So, if we wanted to add a new menu called TM, say to the right of the last existing item, Help, we would add a new command bar to the command bar named Worksheet Menu Bar. To do this we would add a command popup item to the parent command bar. Each popup contains a built-in command bar, which would now be available for our use. Then, if we wanted to add a sub-menu called, say, Excel Memory to the TM menu, we would embed a new command bar within the TM command bar – again by adding a popup item. This submenu would then have some menu items, such as ‘Available memory…” and ‘In use memory’ – see Figure 7. Effectively, we created a command bar (Excel Memory) in a command bar (TM) in a command bar (Worksheet Menu Bar). This should suggest to us that command bars constitute a recursive data structure – and we should explore a recursive routine to add and delete menu items.
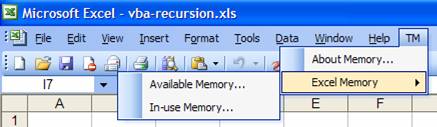
Figure 7
Before we start coding, we will look at the logical
steps needed to create a new menu item.
We need to know three things: (1) the name of the subroutine to be called
when the user selects the menu item, (2) the parent command bar in which the
sub-menus will be nested, and (3) the captions of all the sub-menus and the
final menu item. The first is a
string and we will declare it as such.
The second will be of the data type CommandBar. For the last, we will use an array, with
each element containing the caption of each sub-menu. For convenience (and the reason will
become apparent later), the array will contain the names in the order:
(menu-name, name-of-sub-menu-containing-the-menu,
name-of-sub-menu-containing-sub-menu, …,
highest-sub-menu-name-just-subordinate-to-application-menu). For example, to create the In-use Memory… item in Figure 7, the sequence of names in the array would be ("In-use
Memory...", "Excel Memory", "TM")
We start by declaring the header of the subroutine that will eventually form the core of the recursive program
Sub createMenuUsingStack(AssocSubroutineName As String, _
ParentCmdBar As CommandBar, SubMenuCaptions As Variant)
As one might expect from the discussion in the previous paragraph, the first two arguments are the name of the subroutine to be called (declared as a string) and the parent command bar (declared as a CommandBar). The last item, however, is not of type array, but of type variant. The reason, which will become obvious when we look at more of the code, is that putting an array in a variant makes it easier to code the initial call to this subroutine.
As noted in the comments to the factorial function, each recursive routine has a conditional structure that decides whether the function should be called again, or if it is time to end the recursion. In this case, that will be decided by the contents of the SubMenuCaptions array. If the array contains more than one element, we still have to create additional sub-menus. We create the next sub-menu, remove that element from the array, and recursively call the subroutine with this newly created menu as the new parent and the just truncated array of the remaining names. From the code below, it becomes apparent why we have the sequence of names as we do: the newest sub-menu name is in the highest numbered element of the array and to remove that element from the array, we simply resize the array down by one element.
If ArraySize(SubMenuCaptions) > 1 Then
Dim ChildCmdBar As CommandBar
Set ChildCmdBar = GetaCmdbar( _
ParentCmdBar, CStr(SubMenuCaptions(UBound(SubMenuCaptions))))
ReDim Preserve SubMenuCaptions( _
LBound(SubMenuCaptions) To UBound(SubMenuCaptions) - 1)
createMenuUsingStack AssocSubroutineName, _
ChildCmdBar, SubMenuCaptions
The function GetaCmdBar returns a reference to the desired sub-menu, if it already exists; if the sub-menu does not exist, GetaCmdBar calls addCmdbar to create the sub-menu. addCmdBar, in turn, creates a pop-up control item in the parent command bar, sets its caption, and then returns the command bar embedded within the pop-up control.
The ArraySize function returns the size the array passed to it as the sole argument.[2]
Function addCmdbar(ParentBar As CommandBar, _
NewBarName As String) As CommandBar
Dim IntermediatePopup As CommandBarPopup
Set IntermediatePopup = ParentBar.Controls.Add(msoControlPopup)
IntermediatePopup.Caption = NewBarName
Set addCmdbar = IntermediatePopup.CommandBar
End Function
Function GetaCmdbar(ParentCmdBar As CommandBar, _
SubMenuCaption As String) As CommandBar
Dim RsltBar As CommandBar, TempPopup As CommandBarPopup
On Error Resume Next
Set RsltBar = ParentCmdBar.Controls(SubMenuCaption).CommandBar
If RsltBar Is Nothing Then
Set RsltBar = addCmdbar(ParentCmdBar, SubMenuCaption)
End If
Set GetaCmdbar = RsltBar
End Function
Function ArraySize(SomeArr)
ArraySize = UBound(SomeArr) - LBound(SomeArr) + 1
End Function
On the other hand, if the array contains only one element, it must be the caption of the actual menu item. We should create the actual menu item, set the name of the subroutine to execute when the user selects the menu item, and end the recursion. The code in Code Sample 4 does just that – and includes one more defensive measure. It checks if the menu item is already present; if so, the old item is removed first.
Else
Dim cbButton As CommandBarButton
On Error Resume Next
Set cbButton = ParentCmdBar.Controls( _
SubMenuCaptions(LBound(SubMenuCaptions)))
On Error GoTo 0
If Not (cbButton Is Nothing) Then
cbButton.Delete
End If
Set cbButton = ParentCmdBar.Controls.Add(msoControlButton)
With cbButton
.Caption = SubMenuCaptions(LBound(SubMenuCaptions))
.OnAction = AssocSubroutineName
End With
End If
The code to create the actual menu items is shown below. Note how easy it is to create a menu item as well as creating all the necessary sub-menus. The first createMenuUsingStack() statement creates the TM | About Memory… menu item. The second and third statements create the Available Memory… and the In-use Memory… items respectively. Each is located under the TM | Excel Memory sub-menu.
To add an additional nested sub-menu all one has to do is add its name to the list of names in the Array(…) part. It should also become apparent why SubMenuCaptions above was declared as it was. The Array(…) clause creates a data type that maps very conveniently on to the variant argument.
Sub createCBUsingStack()
createMenuUsingStack _
"AboutMemory", CommandBars("Worksheet Menu Bar"), _
Array("About Memory...", "TM")
createMenuUsingStack _
"AvailMemory", CommandBars("Worksheet Menu Bar"), _
Array("Available Memory...", "Excel Memory", "TM")
createMenuUsingStack _
"InUseMemory", CommandBars("Worksheet Menu Bar"), _
Array("In-use Memory...", "Excel Memory", "TM")
End Sub
The complementary code to remove a menu is similarly recursive. In this case, after removing a menu item (or a sub-menu), one should check if the parent menu has zero controls left, it, too, should be removed. Also, we don’t need any information about the subroutine associated with the menu item. Because of the modular and recursive nature of the existing code, modifying it to our new need is almost trivial. Compare the code in Code Sample 5 with the code in createMenuUsingStack and the similarities will really stand out. Basically, the AssociatedSubroutineName argument is missing. In the code that continues the recursion (i.e., if the size of the SubMenuCaptions array is greater than 1), we have an additional check to delete the submenu if it is empty. The code to manage the last call in the recursion (i.e., when the size of the SubMenuCaptions array is 1) requires only the elimination of the code to create the menu item. The defensive measure we implemented vis-à-vis deleting an existing menu item now becomes the main functional code!
Sub deleteMenuUsingStack( _
ParentCmdBar As CommandBar, SubMenuCaptions As Variant)
If ArraySize(SubMenuCaptions) > 1 Then
Dim ChildCmdBar As CommandBar
Set ChildCmdBar = GetaCmdbar( _
ParentCmdBar, CStr(SubMenuCaptions(UBound(SubMenuCaptions))))
ReDim Preserve SubMenuCaptions( _
LBound(SubMenuCaptions) To UBound(SubMenuCaptions) - 1)
deleteMenuUsingStack _
ChildCmdBar, SubMenuCaptions
If ChildCmdBar.Controls.Count = 0 Then
ChildCmdBar.Parent.Delete
End If
Else
Dim cbButton As CommandBarButton
On Error Resume Next
Set cbButton = ParentCmdBar.Controls( _
SubMenuCaptions(LBound(SubMenuCaptions)))
On Error GoTo 0
If Not (cbButton Is Nothing) Then
cbButton.Delete
End If
End If
End Sub
How is this subroutine used? Analogous to createCBUsingStack, we have deleteCBUsingStack. It is shown in Code Sample 6. Note that the code looks almost identical to that in createCBUsingStack except that it calls the deleteMenuUsingStack subroutine with one fewer argument.
Sub deleteCBUsingStack()
deleteMenuUsingStack _
CommandBars("Worksheet Menu Bar"), _
Array("About Memory...", "TM")
deleteMenuUsingStack _
CommandBars("Worksheet Menu Bar"), _
Array("Available Memory...", "Excel Memory", "TM")
deleteMenuUsingStack _
CommandBars("Worksheet Menu Bar"), _
Array("In-use Memory...", "Excel Memory", "TM")
End Sub
In this chapter, we explored the power of recursion not only
in terms of recursive code, but also the much more overlooked concept of
recursive data structures and the strong connection between the two. In the process we continued the
development of some more practical and very useful functions. The
factorial
function, while trivial and easily replaced by a non-recursive algorithm,
provided an easy basis for understanding recursive code as well as a key
structural component of a recursive subroutine.
We also looked at how easy it is to set up a recursive data structure
with the help of a class module while creating a tree data structure. In the process we learnt a way to implement a
rather efficient sort algorithm. The directory search subsection illustrated
one of the more tricky parts of a recursive program – building an interface
between recursive code and non-recursive people-interface. In the process, we implemented a
practical method for listing all files and folders inside a specified folder,
irrespective of nesting depth.
Finally, we saw the recursive nature of
Office command bars and developed completely function code to create and
remove nested menus in any Office application.
[1] For more on the use of ByRef and ByVal see xxx.
[2] Technically, it returns the size of the first dimension of the array argument.